Compositions

The Twilio Recording Composition API lets you transcode and combine the individual Track Recordings stored by the Twilio Video Recordings API. This API relies on the following REST resources:

• The Composition Instance Resource: a Composition represents a media file created as a result of applying a set of media processing operations onto a number of source Recordings.
• The Compositions List Resource represents the list of previously created Compositions.

These REST resources are located beneath of the following base URL:

1
https://video.twilio.com
2

• URI Schemes
• Composition Instance Resource
  • Resource Properties
  • Get a Composition Instance (HTTP GET)
  • Delete a Composition (HTTP DELETE)
• Composition Instance Media Sub-Resource
  • Get a Composition Media File
• Compositions List Resource
  • Create Composition (HTTP POST)
    • Supported POST Parameters
    • Specifying Video Layouts
    • Region Positioning and Size
    • The Region as a Grid
    • Displaying Video Sources
    • Understanding Reuse
    • Understanding Trim
  • Get lists of Compositions (HTTP GET)
    • Filter Parameters
• Examples
  • Creating Transcoding Compositions
    • Transcode a Video Recording
    • Transcode an Audio Recording
  • Creating Compositions with Simple Layouts
    • Compose one Participant Media
    • Compose one Participant Video with all Room Audios
    • Compose the Complete Room in a Grid
    • Compose a Specific Set of Track Recordings in a Grid
    • Compose a Specific Set of Track Recordings as a Sequence
  • Creating Compositions with Complex Layouts
    • Creating a PiP (Picture-in-Picture) Composition
    • Composing a Room with Natural Layouts
    • Composing a Room with Mosaic Layout
    • Creating a Chess-Table Layout Composition
  • Getting Compositions
    • Get a Composition Instance Resource
    • List a Page of Completed Compositions
    • List all Compositions For a given Room
    • Get a Composition Media File
  • Deleting Compositions
    • Delete a Composition Instance
• Known limitations

These are the URI schemes for the Recording Composition REST API and the supported methods:

• /v1/Compositions/
  • GET: List Composition resources.
  • POST: Create new composition resource.
• /v1/Compositions/{CompositionSid}
  • GET: Retrieve a Composition resource.
  • DELETE: Delete a Composition resource.
• /v1/Compositions/{CompositionSid}/Media
  • GET: Retrieve a Composition media file sub-resource.

A Composition Instance Resource has the following properties

Returns the single Composition identified by {CompositionSid}.

Not supported.

Deletes the media file associated with the Composition identified by {CompositionSID} and sets the Composition status as deleted. In case the media file was stored in an external S3 bucket this request has no effect on such file. Once a Composition has been deleted, its metadata (i.e. it REST resource record) is kept during 30 days.

Retrieves the Composition media file through an HTTP redirection. The format of the provided media file is the one specified in the Format property of the Composition (see table above). By default, the redirection URL is available for 600 seconds, but this can be configured to a value between 1 and 3600 seconds via the Ttl request param. If the composition is not yet available, a 404 is returned.

The HTTP GET request accepts the following parameters

Remark that ContentDisposition affects the content disposition of the redirection URL. This parameter behaves as specified in RFC-6266:

• The value attachment indicates that browsers should prompt the user to store the file locally. In this case, the specification of a filename is mandatory. As shown in the table above, we use this as default and set filename to the Composition SID followed by the format extension. For example, for an MP4 Composition it will take the form CJXXXX.mp4.
• The value inline indicates default processing based on the media type. Hence, whenever the browser supports the composition format, the file will be played. Otherwise, the file is downloaded. Remark that when inline is used it is strongly recommended to provide a filename for the latter case. When doing so, remember that the ContentDisposition parameter must be URLEncoded. For example:

inline%3B%20filename%3D%22MyFile.mp4%22

Not supported.

Not supported.

Creates a new Composition Instance Resource and, when appropriate, launches a media processing task. The result of this task is a composed media file that, by default, is stored in Twilio's cloud.

Developers can create a new Composition as soon as its associated Room exists. However, the processing task gets started only when the Room status is Completed. This guarantees that all required recording sources are available.

This HTTP POST always returns a 201 if the request is accepted (i.e. well formed), and a 4xx otherwise depending on the type of error.

The following table shows all the parameters that can be used when creating a new Composition Instance Resource.

Video layouts are organized in terms of regions. A region is a rectangular area where a set of video sources are displayed following the region placement rules. The VideoLayout of a Composition must contain at least one region but it may contain many. Regions are independent meaning that the way placement works in a region does not affect placement in other regions.

A Composition's VideoLayout is specified as a JSON dictionary of regions following this scheme:

1
VideoLayout = {
2
                "a-region-name": {
3
                    region properties
4
                },
5

6
                "other-region-name": {
7
                  other region properties
8
                }
9

10
                ...
11
              }

The region properties define the size and position of the region, the video sources to include in the region and the placement rules. Regions support the following properties (recall that a "Yes" in the column "Default value/mandatory" indicates a mandatory property)

The use of a VideoLayout not compliant with this specification shall cause the corresponding POST request to be answered with a 4xx code.

The following figure illustrates how regions are positioned:

Expand image

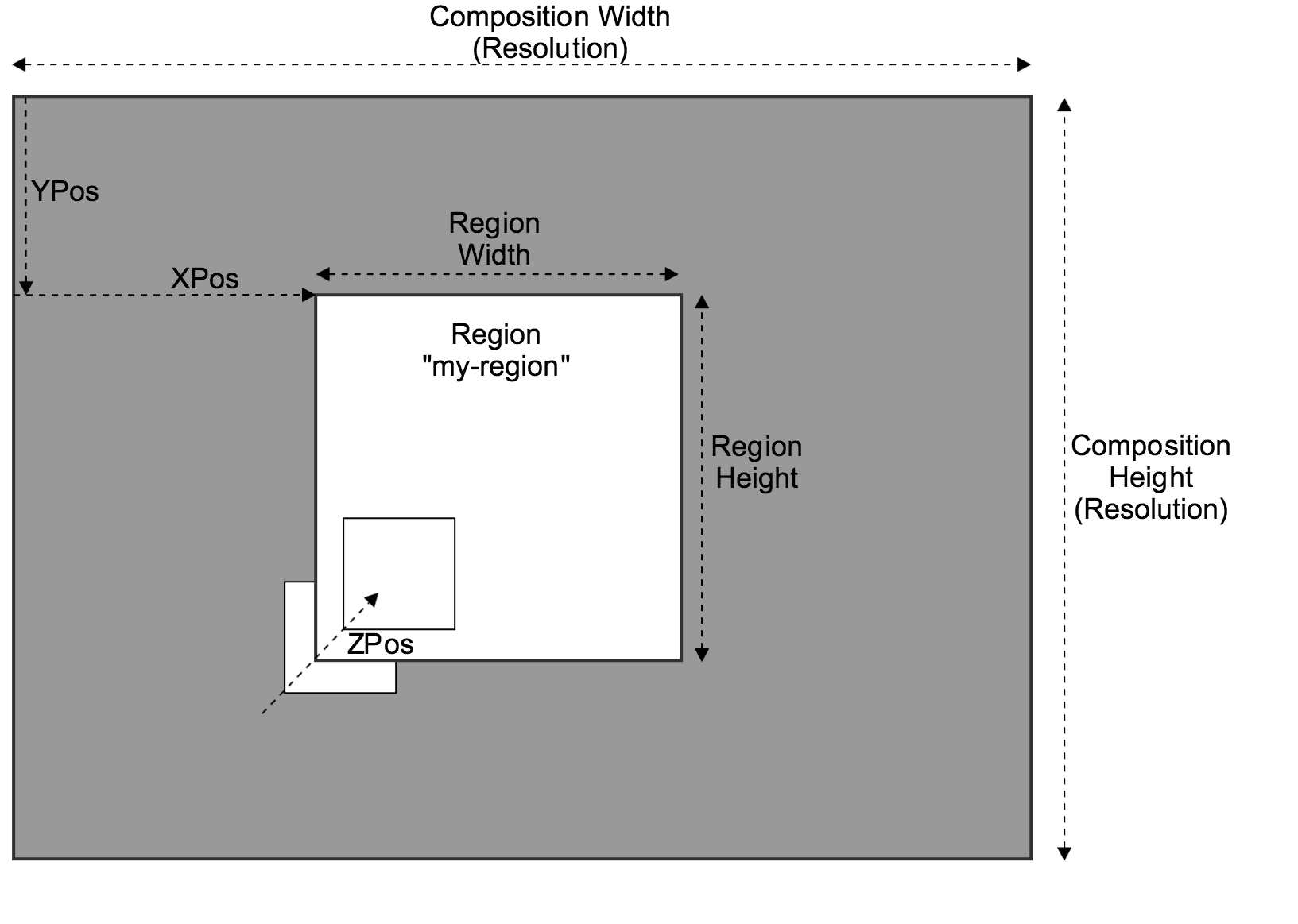
You may find useful to remember these rules:

• The Composition's width and height are defined through the Resolution parameter.
• Regions are positioned relative to the Composition top-left corner using x_pos and y_pos.
• Region dimensions are defined through the width and height properties.
• Regions must fit inside their Composition. This makes the following mandatory:
  • x_pos + width must not be over the Composition's width.
  • y_pos + height must not be over the Composition's height.
• In case width or heightare not specified, by default the region shall occupy all the available remaining space on the Composition's viewport.
• When multiple regions overlap, their visibility depend on the z_pos property. Regions with higher z_pos will be visible on top of regions with lower z_pos.

The placement of video_sources in a region takes place through a grid (i.e. matrix) where every cell is a container where one (and only one) video source may be displayed at a time. Region grids are static meaning that their number of rows and columns do not change during the Composition duration. The specific number of rows and columns depends on the region's max_columns and max_rows properties. There are three different situations:

Expand image

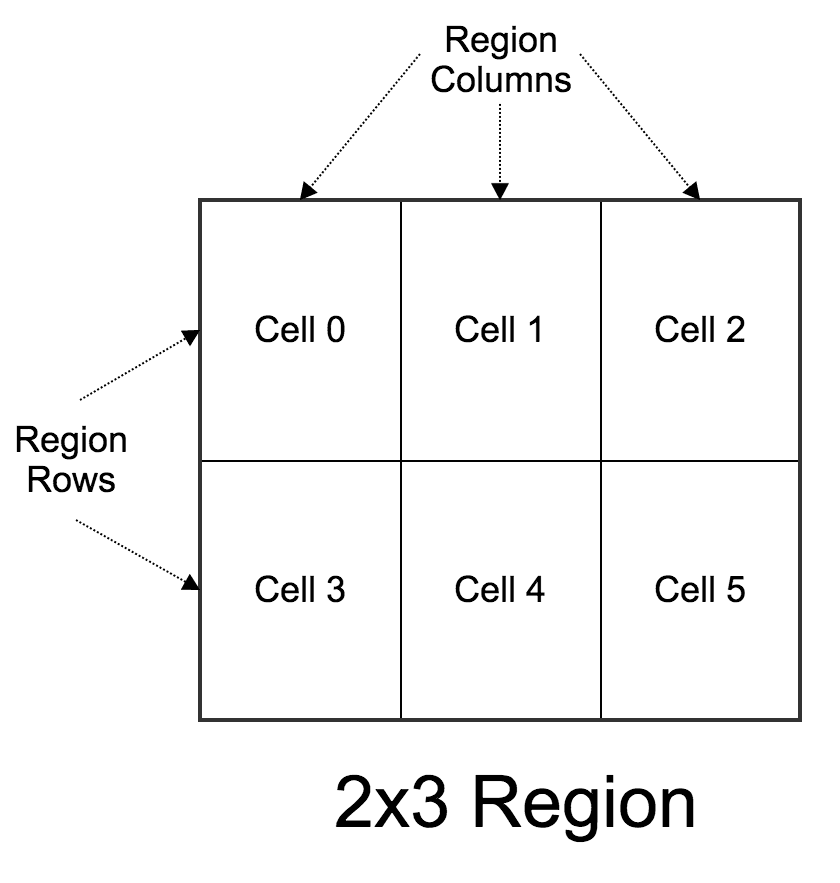
Unconstrained Grid

In this case, neither max_columns nor max_rows are specified in the VideoLayout. Twilio computes for you the grid dimensions to guarantee that all the provided video_sources are displayed. Due to this, the cells in the grid will be at least equal to the maximum number of simultaneous video sources in the Composition (video sources are considered to be simultaneous at a given time when their media is active at that time). For this, we try to keep the grid as square as possible making it to grow first in columns and then in rows so that their difference is never over 1. The following table illustrates this:

Unconstrained Dimension

In this case, only one of max_columns or max_rows is specified. The grid dimensions are computed following the "Unconstrained Grid" algorithm (i.e. trying to keep the grid as square as possible) but without exceeding the specified maximum constraint. After that, the unconstrained dimension grows in order to guarantee that all the specified video sources are displayed. The following examples illustrate this:

Constrained Grid In this case, both max_columns and max_rows are specified. The grid dimensions are computed following the above specified algorithms but keeping both dimensions under their limits. Due to this, the maximum number of cells is max_columns * max_rows. If the number of simultaneous video sources exceeds that value, then some video sources shall not be displayed. The following example illustrates the effect.

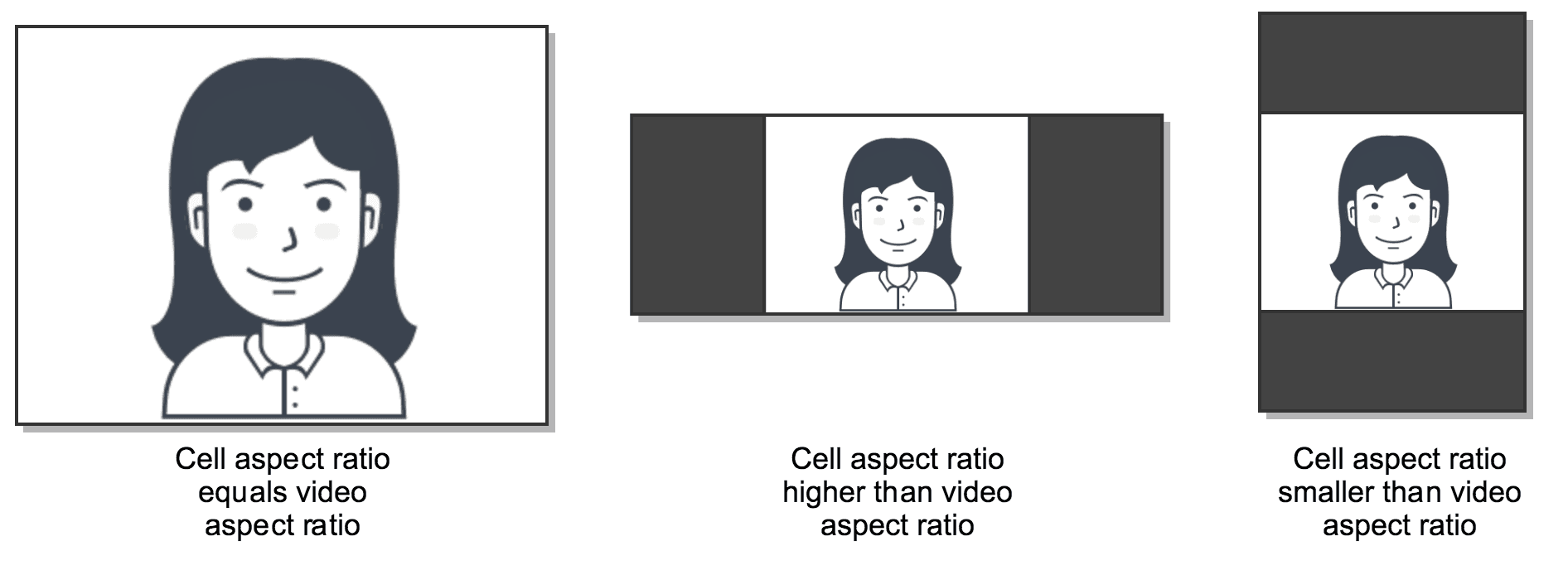
Video sources are displayed in region grid cells. Cells size and aspect ratio is controlled by:

• The region pixel dimensions, as defined by the width and height parameters.
• The region grid dimensions (i.e. number of rows and columns), as introduced in the section above.

Hence, cells would have approximately (rounding effects not considered):

• Width equal to the region's width divided by the number of columns.
• Height equal to the region's height divided by the number of rows.

The display of the original video track sources in cells is performed using "object-fit contain" CSS semantics. This means that the original video is rescaled as necessary to fit into the target aspect ratio and that the remaining areas of the cell are filled in black. The following images illustrate how this happens

Expand image

Video sources are assigned to cells from left-to-right and from top-to-bottom in the region grid. However, this assignment depends on the value of the reuse property. For understanding how reuse works, we need some definitions:

• We say a cell is fresh at a given time when it has not displayed any video source up to that time.
• We say a cell is used at a given time when it is displaying a video source at that time.
• We say a cell is idle at a given time when it has been used previously but its video source media has ended at that time.

Based on this, the possible values for reuse are the following:

• none: in this case, used cells are never reused again and stay idle until the composition ends. Newer video sources are assigned only to fresh cells following the left-to-right top-to-bottom order. In constrained grids, we may run out of fresh cells. In that case, no further video sources are displayed.
• show_oldest: in this case idle cells can be reused. Hence, newer video sources are assigned to both idle or fresh cells in left-to-right top-to-bottom order. In constrained grids, when running out of fresh cells, newer video sources will be displayed only as idle cells become available. In such constrained situation, this model gives display priority to older video sources (i.e. to the video sources starting first), which justifies its show_oldest name.
• show_newest: when this value is specified, video sources are displayed first in idle and fresh cells in the left-to-right top-to-bottom order. In constrained grids it may happen that we run out of both fresh and idle cells. In that case, used cells are reused so that newer video sources are displayed on top of older video sources. When there are several available used cells, the one whose media ends first is selected. As it can be understood, this model gives display priority to newer video sources (i.e. to video sources starting later), which justifies its show_newest name.

The difference between the different reuse modes can be visually appreciated in the following figure:

Expand image

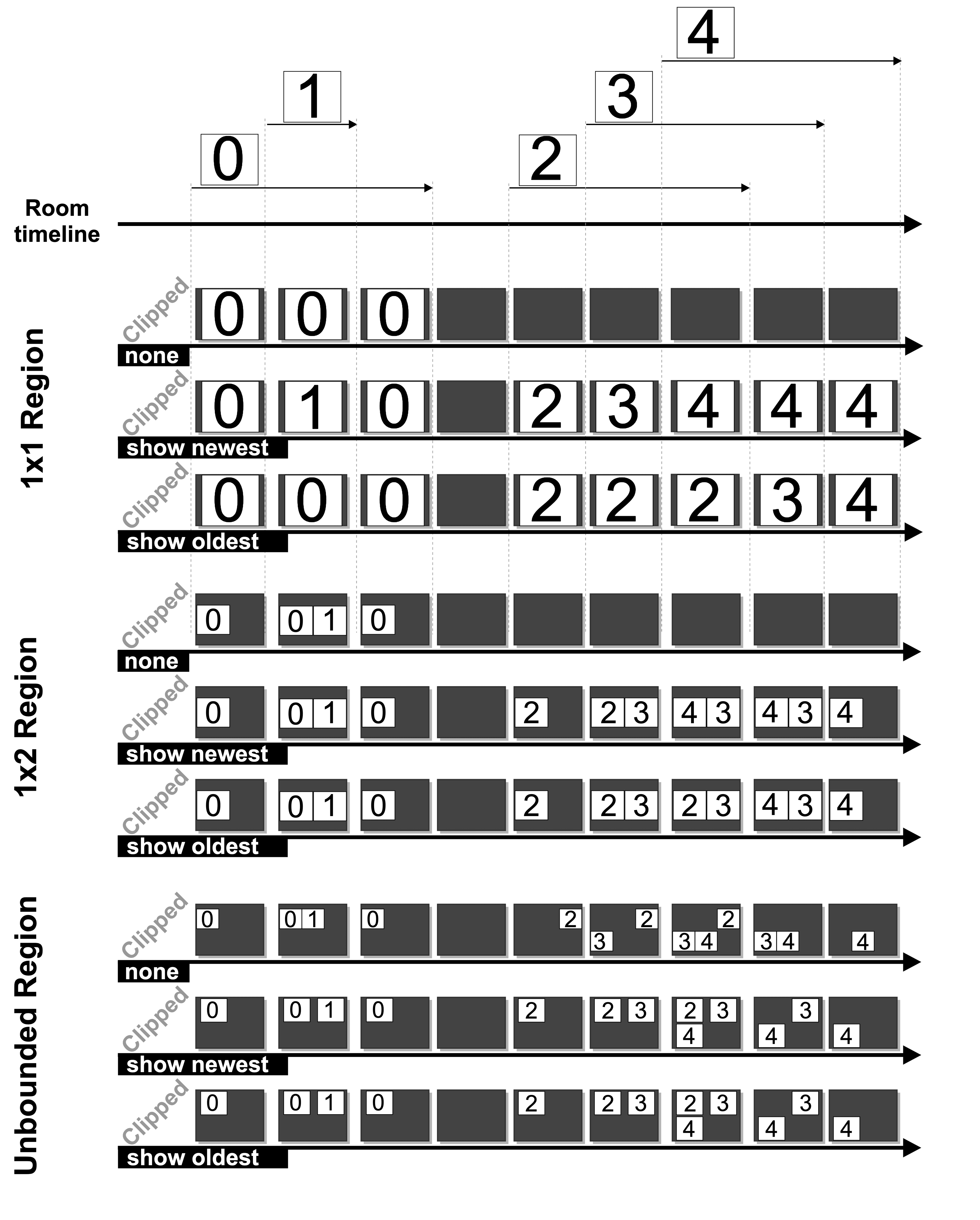
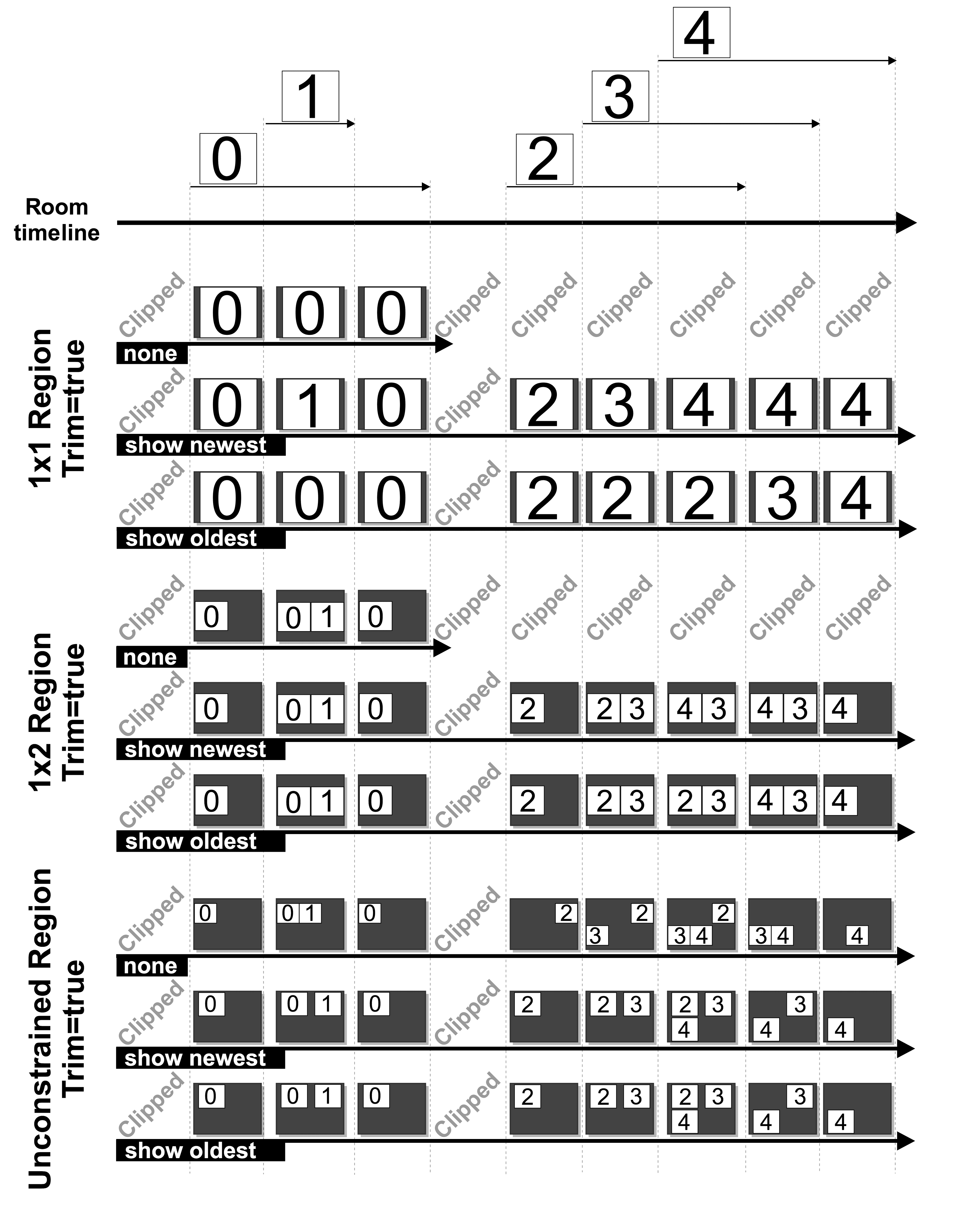
As it can be observed, in this figure we assume a Room with 5 video tracks. These are numbered from 0 to 4. The Room timeline shows the time intervals (relative to the Room starting time) when such tracks are in published state. Below it, we show a number of compositions subject to the following constraints:

• 1x1 Region Composition: in this case, the Composition has a single region where max_rows=1 and max_columns=1. When reuse=none the first track (i.e. the one identified as 0) takes the single fresh cell of the region for display. In the gaps where this track is unpublished, the cell is never reused and the Composition stays black (in case Trim=false) or terminates (in case Trim=true). If reuse=show_newest newer tracks have higher priority than older tracks. Due to this, track 1 is stacked on top of track 0 and displayed while it is active. Later, tracks 2, 3 and 4 take the single region cell as soon as their media is activated. In the case where reuse=show_oldest, the first track occupying the single region cell keeps it until it ends. After that, newer tracks can take it (observe how the end of track 2 allows track 3 to be displayed and how the end of track 3 does the same with track 4.)
• 1x2 Region Composition: now the Composition has a single region with two cells (max_rows=1 and max_columns=2). Due to this, tracks 0 and 1 can be displayed simultaneously. For tracks 2, 3 and 4 their display is controlled by the reuse model. When reuse=none, tracks 0 and 1 take the two fresh cells. After that, no further tracks can reuse such cells and the Composition stays black (in case Trim=false) or terminates (in case Trim=true). If reuse=show_newest 2 and 3 can reuse the idle cells, but when 4 arrives it reuses the used cell with track ending first (in this case 2). When reuse=show_oldest 2 and 3 have priority and hence 4 needs to wait until an idle cell is made available, which takes place when 2 ends.
• Unconstrained Region Composition: in this case, the Composition has a single cell where neither max_rows nor max_columns have been specified. Hence, the region grid dimensions are automatically calculated to fit all the specified video sources. When reuse=none, we need 5 cells given that video sources can only occupy fresh cells. Due to this, the system uses a 2x3 grid. When reuse=show_newest or reuse=show_oldest the required grid needs to have only 3 cells given that the maximum number of simultaneous tracks is 3 (i.e. what happens during the interval in which 2, 3 and 4 are published). Hence, the system computes a 2x2 grid. Observe that when using unconstrained grids, both show_newest and show_oldest generate the same video placement for the region. This is due to the fact that in an unconstrained grid it is guaranteed that the number of video sources never exceeds the number of cells in the grid. Hence, no used cells need ever to be reused.

The Trim Composition parameter controls what happens to the composition when there is no active media. That is, during the gaps in which neither audio tracks nor video tracks are published. We define two types of such gaps:

• Initial gap: Compositions have an initial gap when at the beginning of the Room there is no active media. The initial gap ends when the first recording included in the composition starts. The initial gap is always trimmed in Compositions.
• Later gap: for any other gap not being an initial gap.

Later gaps are trimmed depending on the value of the trim parameter.

• trim=false: The Composition keeps all the later gaps as black video with silent audio. Hence, these idle intervals with no media may appear at the end or in the middle of the Composition.
• trim=true (default): the Composition clips all gaps where there is no media published. Note that when an audio track is active in the composition during an interval it shall not be clipped even if there are no active video tracks on it.

The following figure illustrates how trimmed Compositions behave in the scenarios introduced in the section above.

Expand image

Retrieves the list Composition Instance Records belonging to the specified AccountSid with paging data.

The following GET query string parameters allow you to limit the list returned. Note, parameters are case-sensitive.

Note: deleted Compositions are not returned by default. For retrieving the deleted Compositions list you must explicitly specify Status=deleted.

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where a video Track with MediaTrackSid=MTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX is published and recorded with RecordingTrackSid=RTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX. We want then to generate a Composition containing such video Track but transcoded to the H.264/mp4 format. Considering that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use the default resolution (VGA = 640x480)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    format: "mp4",
13
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
14
    statusCallback: "https://www.example.com/callbacks",
15
    videoLayout: {
16
      transcode: {
17
        video_sources: ["RTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"],
18
      },
19
    },
20
  });
21

22
  console.log(composition.accountSid);
23
}
24

25
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1920x1080",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where an audio Track with MediaTrackSid=MTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX is publishes and recorded with RecordingTrackSid=RTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX. We want then to generate a Composition containing such audio Track but transcoded to the AAC/mp4 format. Considering that:

• Your application credentials are (SKXXXX:your_api_key_secret)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    audioSources: ["RTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"],
13
    format: "mp4",
14
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
15
    statusCallback: "https://www.example.com/callbacks",
16
  });
17

18
  console.log(composition.accountSid);
19
}
20

21
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1920x1080",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

Remark that, in spite of this being an only-audio composition, it shows default video settings in the corresponding response parameters.

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where a Participant with ParticipantSid=PAXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX publishes both audio and video tracks to the Room. In this Room there may be other Participants publishing audio and video without affecting this example's result.

We want to generate a Composition showing the Participant's video Track and having as audio the one of that Participant. Considering that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use mp4 as target format
• You want to use the default resolution (VGA = 640x480)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    audioSources: ["PAXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"],
13
    format: "mp4",
14
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
15
    statusCallback: "https://www.example.com/callbacks",
16
    videoLayout: {
17
      single: {
18
        video_sources: ["PAXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"],
19
      },
20
    },
21
  });
22

23
  console.log(composition.accountSid);
24
}
25

26
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1920x1080",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where a Participant with ParticipantSid=PAXXXX publishes both audio and video Tracks. In that Room others participant publish also their audio and video Tracks. We want generate a Composition showing PAXXXX video but having as audio the complete set of Room audio Tracks mixed. Considering that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use mp4 as target format
• You want to use the default resolution (VGA = 640x480)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    audioSources: ["*"],
13
    format: "mp4",
14
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
15
    statusCallback: "https://www.example.com/callbacks",
16
    videoLayout: {
17
      single: {
18
        video_sources: ["PAXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"],
19
      },
20
    },
21
  });
22

23
  console.log(composition.accountSid);
24
}
25

26
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1920x1080",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where multiple Participants publish both audio and video Tracks. We want generate a Composition showing all the room videos in a grid, as shown in the figure below, and with all audio tracks mixed.

Expand image

Considering that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use mp4 as target format
• You want to use VGA resolution (640x480)
• You want an unconstrained grid composition with the default cell reuse strategy (show_oldest).

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    audioSources: ["*"],
13
    format: "mp4",
14
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
15
    statusCallback: "https://www.example.com/callbacks",
16
    videoLayout: {
17
      grid: {
18
        video_sources: ["*"],
19
      },
20
    },
21
  });
22

23
  console.log(composition.accountSid);
24
}
25

26
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1920x1080",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where different Participants publish their audio and video Tracks. Imagine that we have special interest in some of these tracks that we identify in the following way:

• RTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX: the RecordingTrackSid of a video Track.
• MTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX: the MediaTrackSid of a video Track.
• teacher-webcast: the Track name of a video track.

We want to generate a composition showing the three video Tracks in a single row and with no audio, as shown in the figure below.

Expand image

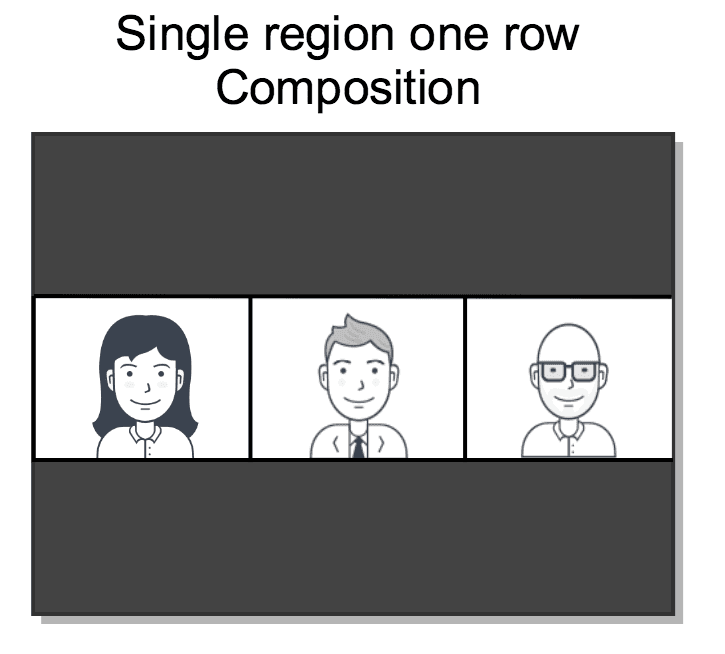
Considering that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use mp4 as target format
• You want to use the default resolution (VGA = 640x480)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    format: "mp4",
13
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
14
    statusCallback: "https://www.example.com/callbacks",
15
    videoLayout: {
16
      grid: {
17
        max_rows: 1,
18
        video_sources: [
19
          "RTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX",
20
          "MTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX",
21
          "teacher-webcast",
22
        ],
23
      },
24
    },
25
  });
26

27
  console.log(composition.accountSid);
28
}
29

30
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1920x1080",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where a teacher presents lessons to their students. These lessons consist on talks and screensharing presentations that occur in sequence. These may overlap or have idle intervals where no media is published. The Track names of the published media comply with the following pattern:

• For video: teacher-video-sess-1, teacher-video-sess-2, etc.
• For audio: teacher-audio-sess-1, teacher-audio-sess-2, etc.

In this context, we want to create a Compositions showing only one video source at a time. That one must match with the video track published later by the teacher at any time. We want the teacher's audio to be included in the Composition. We don't want the Composition to contain the idle intervals where the teacher is not publishing media. In this context, considering that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use mp4 as target format
• You want to use the default resolution (VGA = 640x480)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    audioSources: ["teacher-audio-sess-*"],
13
    format: "mp4",
14
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
15
    statusCallback: "https://www.example.com/callbacks",
16
    videoLayout: {
17
      sequence: {
18
        max_rows: 1,
19
        max_columns: 1,
20
        reuse: "show_newest",
21
        video_sources: ["teacher-video-sess-*"],
22
      },
23
    },
24
  });
25

26
  console.log(composition.accountSid);
27
}
28

29
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1920x1080",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where an expert presents a topic with two audio tracks:

• One track is from his microphone and has the MediaTrackSid=MTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
• One acting as a background soundtrack with Track name =soundtrack

He also has two video tracks:

• A webcam video track with MediaTrackSid=MTYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY
• A screensharing video Track with Track name screen-presentation.

In this context, we want to create a PiP Composition including the above mentioned audio Tracks and showing:

• The video track screen-presentation occupying the complete Composition background.
• The video track MTYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY in a small box located at the top-left corner of the Composition overlayed on top of screen-presentation as shown on the figure below.

Expand image

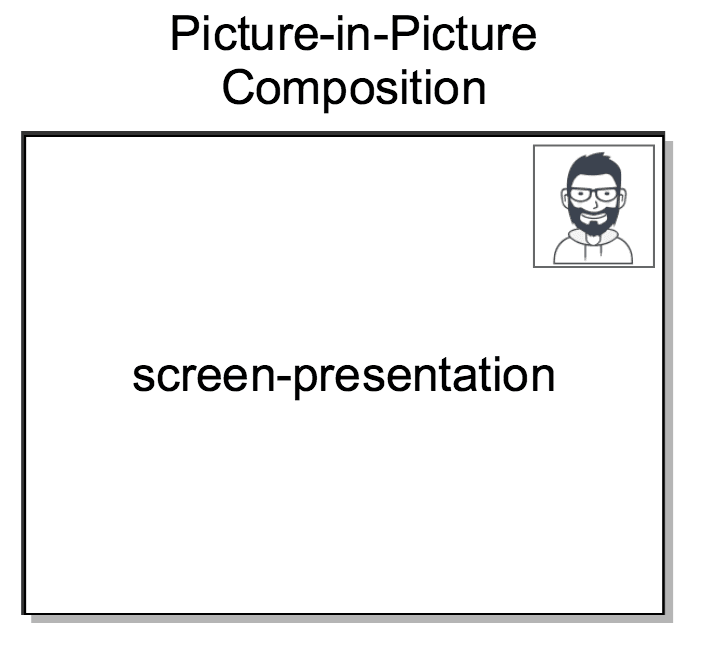
Assuming that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use mp4 as target format
• You want to use HD resolution (1280x720)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    audioSources: ["MTXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX", "soundtrack"],
13
    format: "mp4",
14
    resolution: "1280x720",
15
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
16
    statusCallback: "https://www.example.com/callbacks",
17
    videoLayout: {
18
      main: {
19
        z_pos: 1,
20
        video_sources: "screen-presentation",
21
      },
22
      pip: {
23
        z_pos: 2,
24
        x_pos: 1000,
25
        y_pos: 30,
26
        width: 240,
27
        height: 180,
28
        video_sources: ["MTYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY"],
29
      },
30
    },
31
  });
32

33
  console.log(composition.accountSid);
34
}
35

36
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1280x720",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

In this example we assume a Room with RoomSid=RMXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX where a lecture is taking place. The Participants are the following:

• A teacher publishes the following Tracks:
  • A webcam video Track with name teacher-webcam-video.
  • An screensharing video Track with name teacher-screen-video.
  • An audio Track with name teacher-audio.
• A variable number of students publishing each the following (i varies from student to student):
  • A webcam video track with name student-i-video
  • An audio Track with name student-i-audio

In this context, imagine that we want to create the following Composition:

• Track teacher-screen-video must be shown as Composition background occupying its complete viewport. A track with such disposition is sometimes called "main".
• The rest of video tracks should be shown in a row at the bottom of the Composition, as shown in the figure below.
• All the audio tracks of the Room should be mixed for the Composition.

Expand image

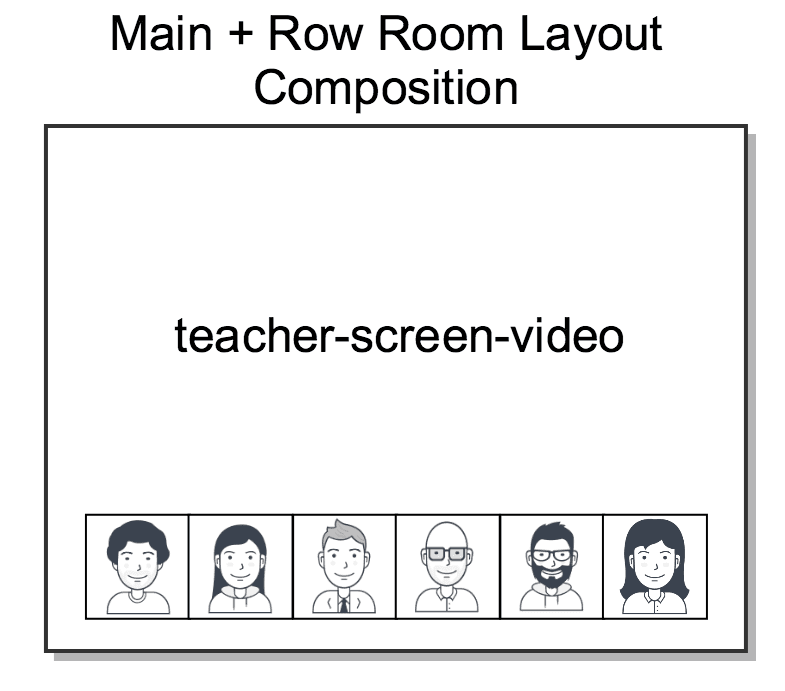
Assuming that:

• Your application credentials are (SKXXXX:your_api_key_secret)
• You want to use mp4 as target format
• You want to use HD resolution (1280x720)

You can create the desired Composition using the following:

1
// Download the helper library from https://www.twilio.com/docs/node/install
2
const twilio = require("twilio"); // Or, for ESM: import twilio from "twilio";
3

4
// Find your Account SID and Auth Token at twilio.com/console
5
// and set the environment variables. See http://twil.io/secure
6
const accountSid = process.env.TWILIO_ACCOUNT_SID;
7
const authToken = process.env.TWILIO_AUTH_TOKEN;
8
const client = twilio(accountSid, authToken);
9

10
async function createComposition() {
11
  const composition = await client.video.v1.compositions.create({
12
    audioSources: ["*"],
13
    format: "mp4",
14
    resolution: "1280x720",
15
    roomSid: "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
16
    statusCallback: "https://www.example.com/callbacks",
17
    videoLayout: {
18
      main: {
19
        z_pos: 1,
20
        video_sources: ["teacher-screen-video"],
21
      },
22
      row: {
23
        z_pos: 2,
24
        x_pos: 10,
25
        y_pos: 530,
26
        width: 1260,
27
        height: 160,
28
        max_rows: 1,
29
        video_sources: ["*"],
30
        video_sources_excluded: ["teacher-screen-video"],
31
      },
32
    },
33
  });
34

35
  console.log(composition.accountSid);
36
}
37

38
createComposition();

1
{
2
  "account_sid": "ACaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
3
  "status": "processing",
4
  "date_created": "2015-07-30T20:00:00Z",
5
  "date_completed": null,
6
  "date_deleted": null,
7
  "sid": "CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
8
  "room_sid": "RMaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
9
  "audio_sources": [
10
    "RTaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
11
    "user*"
12
  ],
13
  "audio_sources_excluded": [
14
    "RTbaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
15
  ],
16
  "video_layout": {
17
    "custom": {
18
      "video_sources": [
19
        "user*"
20
      ],
21
      "video_sources_excluded": [
22
        "RTcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
23
      ],
24
      "reuse": "show_oldest",
25
      "x_pos": 100,
26
      "y_pos": 600,
27
      "z_pos": 10,
28
      "width": 800,
29
      "height": 0,
30
      "max_columns": 0,
31
      "max_rows": 0,
32
      "cells_excluded": [
33
        2,
34
        3
35
      ]
36
    }
37
  },
38
  "trim": true,
39
  "format": "mp4",
40
  "resolution": "1280x720",
41
  "bitrate": 0,
42
  "size": 0,
43
  "duration": 0,
44
  "media_external_location": null,
45
  "encryption_key": null,
46
  "url": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
47
  "status_callback": "https://www.example.com/callbacks",
48
  "status_callback_method": "POST",
49
  "links": {
50
    "media": "https://video.twilio.com/v1/Compositions/CJaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa/Media"
51
  }
52
}

Imagine now that you want the Composition to have a slightly different layout:

• Track teacher-screen-video must be shown as Composition background occupying its complete viewport.
• Track teacher-webcam-video must be shown as a small window in the top-right corner of the Composition.
• The rest of video tracks should be shown in a column on the left with no more than 5 rows as shown on the figure below.
• All the audio tracks of the Room should be mixed for the Composition.

Expand image

In this case, the required code would be the following: