Intro to Markov Models with Swift
Time to read:

Did you know PageRank, the algorithm Google uses to determine the order of search results, is a type of Markov chain? I first learned about Markov chains and Markov models in my Speech Synthesis and Recognition elective and was amazed at how they are used in speech recognition, music generation, and modeling sequential data to predict the outcome of a basketball game (or almost any competition.)
What are Markov Chains and Markov Models?
The most basic type of Markov model is a Markov chain, a model whose next state is only selected based on its current state. Markov chains are used in genetics, finance, economics, game theory, and other fields. An example of one would be predicting tomorrow's weather by looking only at today's weather, not yesterday's.

Wikipedia defines a Markov model like so:
In probability theory, a Markov model is a stochastic model used to model randomly changing systems where it is assumed that future states depend only on the current state, not on the events that occurred before it (that is, it assumes the Markov property).
The transition from one state to another satisfies the Markov Property. It states that the probability of transitioning to any other state is only based on the current state, and not on the sequence of states that came before it--thus every Markov process is memoryless.
Hidden Markov models are a type of Markov chain where some states are observable and some are hidden. They are sometimes explained by the Ice Cream Climatology scenario, proposed by Jason Eisner in 2002:
The situation: You are a climatologist in the year 2799, studying the history of global warming. You can't find any records of Baltimore weather, but you do find my (Jason Eisner's) diary, in which I assiduously recorded how much ice cream I ate each day. What can you figure out from this about the weather that summer?

I recently thought, "what would be the Twilio way of explaining this concept?" Since developers are DOers let's show, not tell, an example.
Sample Sentence
Let's break down a sentence that means something to Twilio: Never gonna give you up. Never gonna let you down.

This has ten words (also known as tokens) and seven unique words (also known as keys.) A weighted distribution is the percentage that one key will appear. It is based on the total amount of times a key shows up divided by the total number of tokens. "Never", "gonna", and "you" all have a weighted distribution of 2/10, as shown in the histogram below.
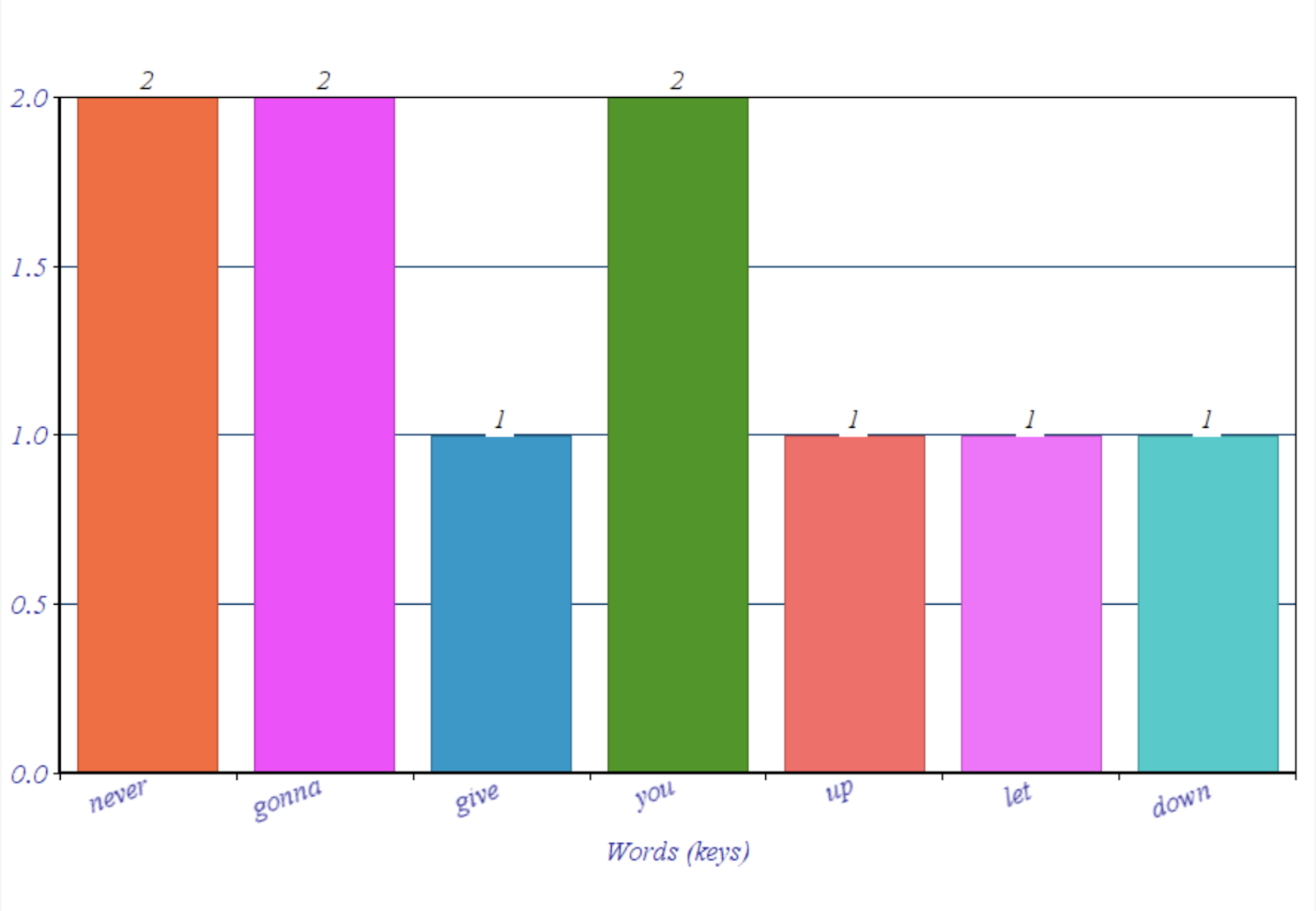
Histograms are a simple way to represent weighted distributions. These keys, or words, can also represent states. Each key can point to another key: this is called a transition.
Transitioning Between States
Let's visualize how every key is matched with an array of possible tokens that could follow that key.
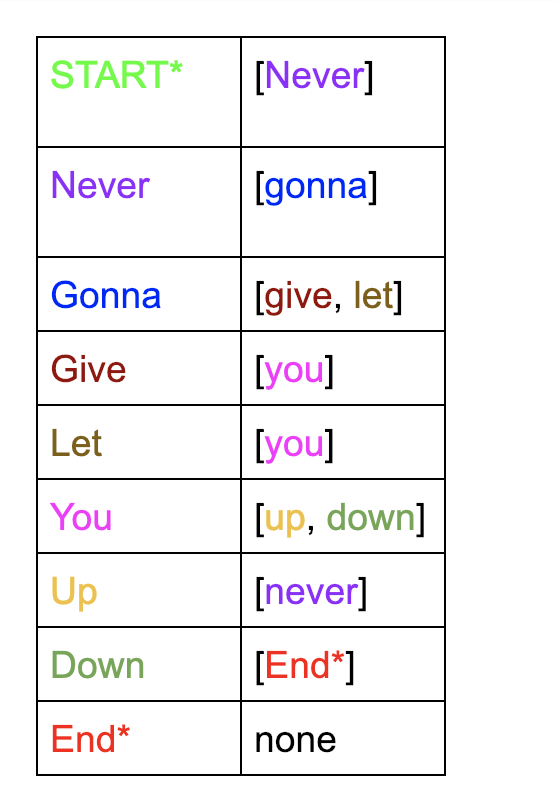
Here, the tokens are organized in pairs with a state corresponding to the possible states that can follow it. How can this better be visualized?
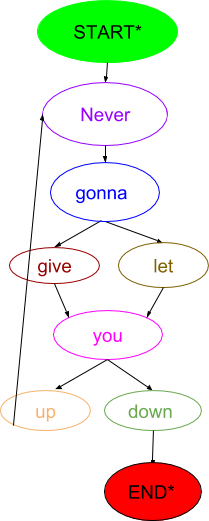
In the above graphic, each word represents a key, or a state, and the arrows point to potential states that can follow it. The corresponding color-coded sentence looks like this:

But wait! There's more!

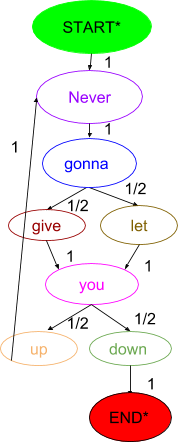
Let's try adding the weighted distributions so that each arrow has the probability that it will be selected as the transition to the next state.
Using CocoaPods with Swift Playgrounds
Swift Playgrounds are amazing at letting you see the results of your code quickly. We'll be using them in addition to a Swift library called MarkovModel to visualize our Markov model example via code.
To use CocoaPods with Playgrounds, first create a new directory and then make a new XCode project there. On the command line in the top level of your directory, make a podfile with pod init and include this code in it:
Back on the command line run pod install, and close the project. Next, create a Swift Playground by opening Xcode and clicking File->New->Playground and saving it in the top level of your directory. If you don't see the playground, drag it into the workspace like so:
Now make sure you open up your .xcworkspace and not .xcproject and place the following starter code in your .playground file to check that the pod installed correctly.
You may need to clean with cmd-shift-k and then build with cmd-b, but should be good to go!
Markov Models with Swift
Let's translate our rickrolling sentence into Swift code using methods from the MarkovModel library.
Here, we create a Markov model to train and pass it an array of the tokens from our sentence. We calculate a future state by calling next. With this library we have three possible decision process options: predict, random and weightedRandom. The default is predict.
You can also print out the weighted distributions of each token with:
Wow! Markov chains are so powerful. As a Golden State Warriors fan, I wonder about trying to predict the outcome of their games based on prior games, or maybe how Steph Curry will shoot based on previous statistics. Think of the other possibilities--they're endless!
For more resources to learn about Markov chains and models, I recommend this Clemson University lecture or UC Davis one, and this interactive explanation of Markov Chains and Khan Academy video.
Stay tuned for the next post where we will train a Markov model with different inputs to generate similar text. In the meantime, let me know how you would use Markov models in the comments, on Twitter or GitHub or via email at lsiegle@twilio.com!
Related Posts
Related Resources
Twilio Docs
From APIs to SDKs to sample apps
API reference documentation, SDKs, helper libraries, quickstarts, and tutorials for your language and platform.
Resource Center
The latest ebooks, industry reports, and webinars
Learn from customer engagement experts to improve your own communication.
Ahoy
Twilio's developer community hub
Best practices, code samples, and inspiration to build communications and digital engagement experiences.


